(1). pgs lingkaran yang tegak lurus garis
4. Diberikan lingkaran x2+y2=10, A(4,-3) dan B(-8,1). Persamaan garis singgung dari lingkaran yang tegak lurus dengan garis AB adalah ….
A. y=3x±10 D. y=-x±10√10
B. y=3x±10√10 E. y=-⅓x±10
C. y=-3x±10
Jawab: A Bahas:
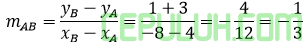
Hasil kali gradien garis tegak lurus =-1
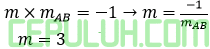
Bentuk persamaan lingkaran
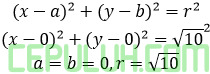
PGS lingkaran
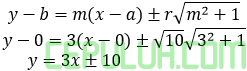
(2). persamaan garis singgung yang tegak lurus garis
7. Salah satu persamaan garis singgung lingkaran x2+y2-4x-8y+15=0 yang tegak lurus garis x+2y=6 adalah ….
A. 2x–y+3=0
B. 2x–y+5=0
C. 2x–y+7=0
D. 2x–y+13=0
E. 2x–y+25=0
Jawab: Bahas:
Bentuk persamaan lingkaran
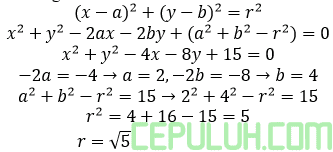
Sejajar maka gradien garis singgung sama dengan gradien garis lain
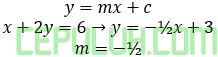
Syarat tegak lurus
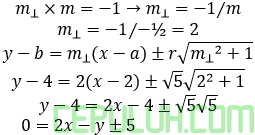
Dua PGS lingkaran
0=2x-y-5
(3). pgs lingkaran yang tegak lurus sebuah garis
9. Persamaan garis singgung lingkaran x2+y2-2x-4y=0 yang tegak lurus garis 2x–y+3=0 adalah:
A. x+2y-3=0
B. 2x+y+1=0
C. x+2y-10=0
D. x-2y-1=0
E. 2x–y-1=0
Jawab: C Bahas:
Hasil kali gradien garis tegak lurus =-1.
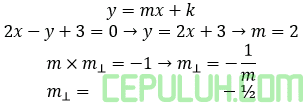
Bentuk persamaan lingkaran
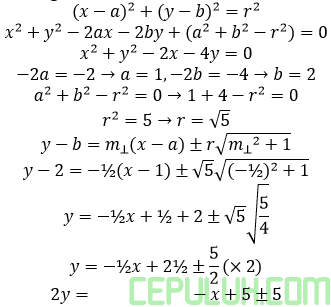
PGS I x+2y=5+5→x+2y-10=0
PGS II x+2y=5-5→x+2y=0
(4). Persamaan garis singgung lingkaran
10. Persamaan garis singgung lingkaran x2+y2-6x+8y-7=0 yang tegak lurus x+y=1 sama dengan:

jawab: C
Hasil kali gradien garis tegak lurus =-1.
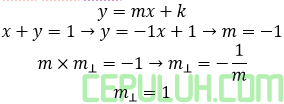
Bentuk persamaan lingkaran
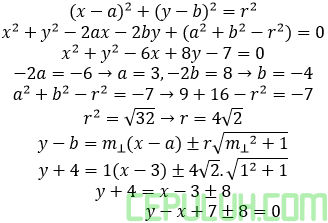
PGS I y–x+7+8=0→y–x+15=0
PGS II y–x+7-8=0→y–x-1=0
(5). persamaan garis singgung lingkaran yang tegak lurus garis
3. Persamaan garis singgung pada lingkaran x2+y2-2x+4y-4=0 yang tegak lurus garis 3x-4y-5=0.
A. 4x+3y+(2±15)=0
B. 4x-3y+(2±15)
C. 4x+3y-(2±15)
D. 4x-3y-(2±15)
E. 4x+3y-2=0
Jawab: A Bahas:
Hasil kali gradien garis tegak lurus =-1.
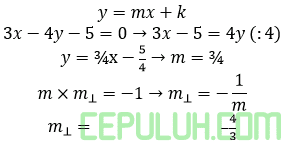
Bentuk persamaan lingkaran
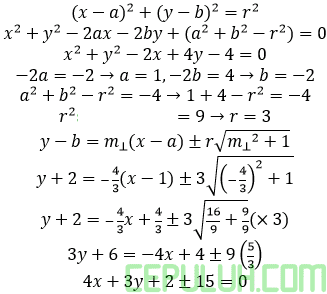
(6). Persamaan Garis Singgung Lingkaran yang Sejajar or Tegak Lurus Garis
Persamaan Garis Singgung Lingkaran PGSL Sejajar Garis
Persamaan Garis Singgung Lingkaran PGSL: Gradien; Sudut