(1). Soal Nilai Maksimum Program Linear
Contoh soal menghitung nilai maksimum dari daerah penyelesaian program linear.
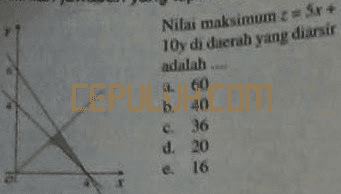
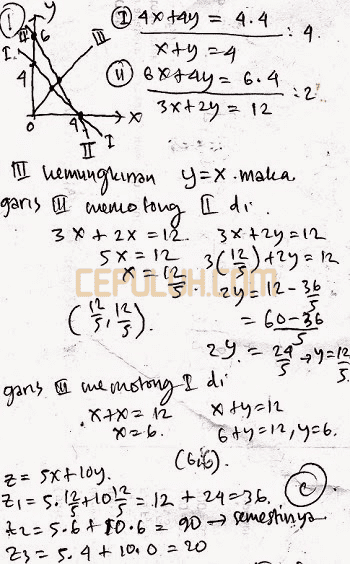
Contoh soal ceritam enghitung nilai maksimum.

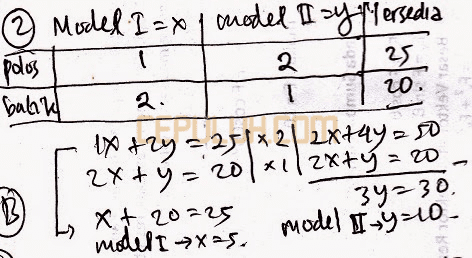


Contoh soal mencari letak nilai maksimum pada grafik program linear.

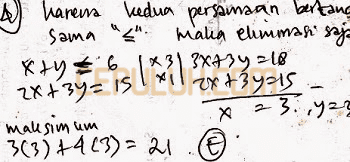
(2). Keuntungan Terbesar dengan Program Linear
Setiap hari seorang pengrajin tas memproduksi dua jenis tas. Modal untuk tas model I adalah Rp20.000,00 dengan keuntungan 40%. Modal untuk tas model II adalah Rp30.000,00 dengan keuntungan 30%. Jika modal yang tersedia setiap harinya adalah Rp1.000.000,00 dan paling banyak hanya dapat memproduksi 40 tas, keuntungan terbesar yang dapat dicapai pengrajin tas tersebut adalah ….
Jawab: B Bahas:
Banyak tas model I x, model II y.
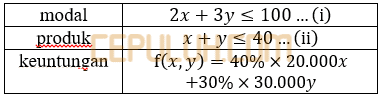
Nilai maksimum dua pertidakasamaan bertanda ≤ adalah nilai fungsi objek dari titik potong keduanya.
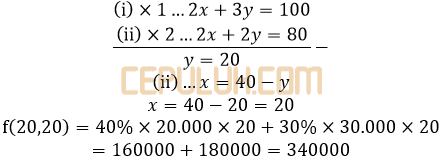
Persen keuntungan P.
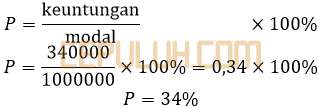
Banyak pakaian wanita jenis A dan jenis B yang terjual berturut-turut adalah 30 dan 16.
(3). Program Linear Keuntungan Maksimum
Perusahan mebel memproduksi dua model meja makan. Biaya untuk membuat tiap meja makan model A adalah Rp1.200.000,00 sedangkan untuk meja makan model B adalah Rp1.600.000,00. Waktu yang diperlukan untuk membuat setiap meja makan model A adalah 2 hari dan tiap meja makan model B adalah 5 hari. Modal yang tersedia sebesar Rp22.000.000,00 dan waktu yang tersedia adalah 60 hari. Keuntungan tiap meja makan model A adalah Rp1.000.000,00 sedangkan tiap meja makan model B adalah Rp1.500.000,00. Keuntungan maksimum yang dapat diperoleh adalah ….
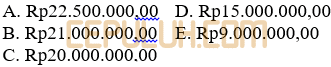
Jawab: C Bahas:
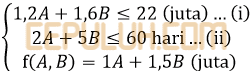
Jika tanda sama ≤ maka keuntungan maksimum di dapat dengan memasukkan titik potong kedua persamaan ke fungsi objek. Eliminasi A.
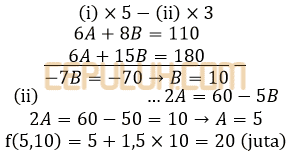
(4). Hasil Penjualan Maksimum dari Fungsi Objektif
Pesawat udara mempunyai tempat duduk 58 kursi. Setiap penumpang kelas utama boleh membawa bagasi 60 kg sedang kelas ekonomi 20 kg. Pesawat hanya mampu membawa bagasi 1.440 kg. Harga tiket kelas utama Rp750.000,00 dan kelas ekonomi Rp500.000,00. Hasil dari penjualan tiket maksimum adalah ….

Jawab: C Bahas:

Jika kedua persamaan bertanda ≤ maka nilai maksimumnya didapat dengan memasukkan titik potongnya ke fungsi objekti. Eliminasi y dengan (ii)-(i).
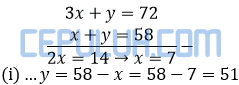
fungsi objektif di sini adalah fungsi penjulan tiket.
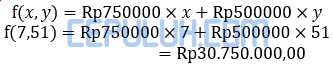
(5). Program Linear Keuntungan Terbesar
Setiap hari seseorang pengrajin tas memproduksi dua jenis tas. Modal untuk tas model I adalah Rp20.000,00 dengan keuntungan 40%. Modal untuk tas model II adalah Rp30.000,00 dengan keuntungan 30%. Jika modal yang tersedia setiap harinya adalah Rp1.000.000,00 dan paling banyak hanya dapat memproduksi 40 tas, keuntungan terbesar yang dapat dicapai pengrajin tas tersebut adalah ….
Jawab: B Bahas:
Banyak tas model I x, model II y.
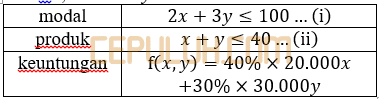
Nilai maksimum dua pertidakasamaan bertanda ≤ adalah nilai fungsi objek dari titik potong keduanya
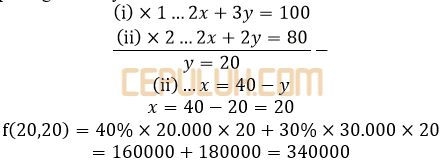
Persen keuntungan P.
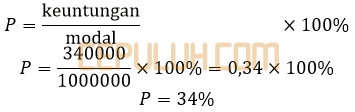
(6). Laba Maksimum
Seorang pengusaha mainan anak-anak akan membeli beberapa boneka Barbie dan boneka Masha tidak lebih dari 25 buah. Harga sebuah boneka Barbie Rp60.000,00 dan harga sebuah boneka Masha Rp80.000,00. Modal yang dimiliki pengusaha Rp1.680.000,00. Jika laba penjualan 1 boneka Barbie Rp20.000,00 dan 1 boneka Masha Rp25.000,00, maka laba maksimumnya adalah ….
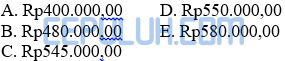
Jawab: C Bahas:
Banyak boneka Barbie x dan boneka Masha y.
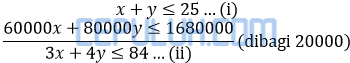
Jika kedua persamaan bertanda ≤ maka nilai maksimumnya didapat dengan memasukkan titik potongnya ke fungsi objekti. Eliminasi x dengan (ii)-(i)×3.
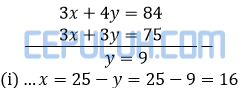
fungsi objektif di sini adalah fungsi laba.
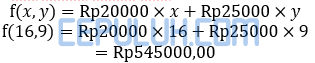
Hasil Maksimum Fungsi Objektif